IterMethods

[TOC]

目录和划重点表

本文为：Iterative Methods for SparseLinear Systems--Second Edition 的读书笔记。 作者是Yousef Saad。年份是2003.

首先大致来看下目录

第一章 线性代数

第二章 PDE离散化

第三章 稀疏矩阵

第四章 基础迭代法

第五章 投影法

第六章 Krylov子空间法I

第七章 Krylov子空间法II

第八章 法线方程组方法

第九章 预处理迭代法

第十章 预处理技术

第十一章 并行的实现

第十二章 并行的预处理

第十三章 多重网格

第十四章 区域分解法

实际上，这本书是同时面向数学专业和计算机专业的。对于CS的学生来说，许多章节可以被跳过，还有一些章节只需要略读。下面是一章教学表格。Quarter Course旨在20节75分钟的课程内完成。我们就照着这张表来读书。

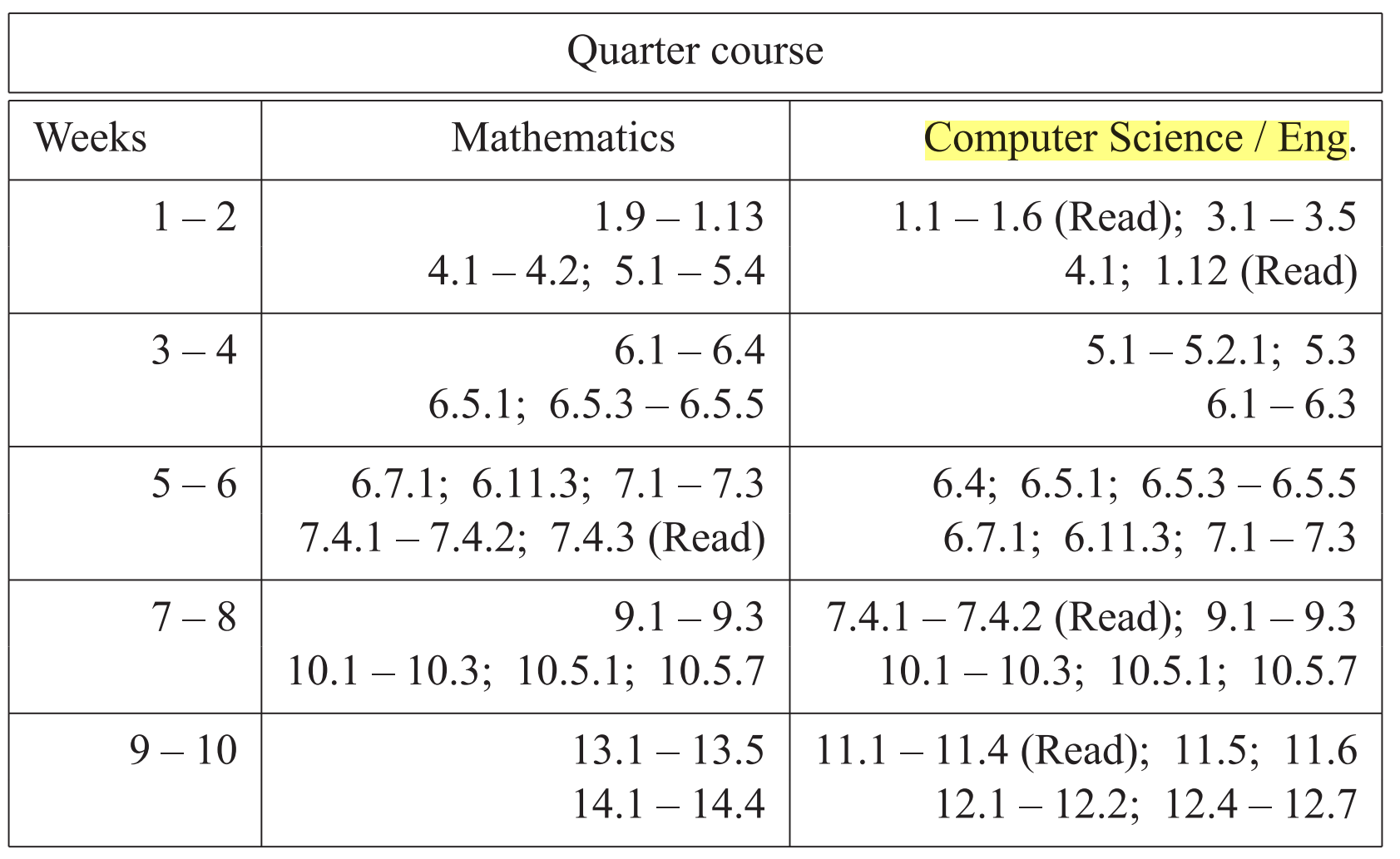
第一章节 线性代数背景知识

需要阅读的为1.1-1.6。另外1.8.1，1.8.3，1.8.4，1.9也比较重要。1.12推荐在学习第五章之前阅读。

因为1.1-1.6都是矩阵的基本概念，我们这里跳过。

1.8是矩阵的规范形式

1.8.1 还原到对角形式

1.8.3 Schur规范形式

1.8.4 应用于矩阵的幂

1.9 正规和Hermitian矩阵

1.6 子空间、范围和核

子空间是什么？

某个空间Cn的子空间就是一组向量的集合。这组向量要满足一个关系：

不那么严谨地说就是：

Cn内的任意一个向量都能用其子空间的线性组合得到。

严谨一点即

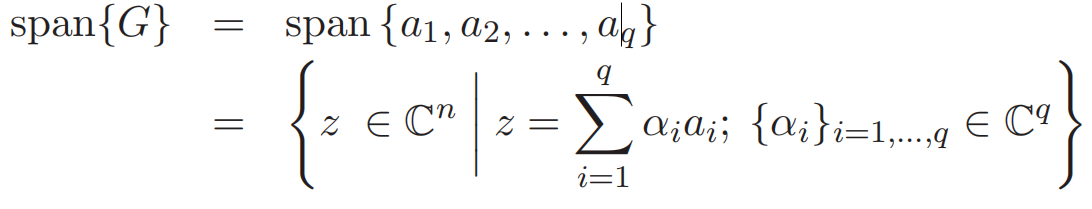
范围是什么？

范围和核(也叫零空间)是两种特殊的子空间。他们都是对着矩阵A来说的。A是mxn矩阵。

范围（range) 是

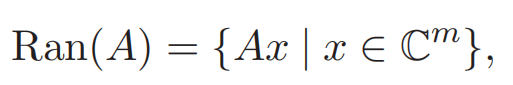
也就是经过矩阵变换之后的任意向量的集合。

通俗来说：子空间是原空间的线性组合，这个线性组合取一个矩阵，那就是范围。。

从直观上讲，A的范围就是Ax=b中的b所张成的空间。

核是什么？

核（kernel)也叫零空间（Null space)

$$Null(A) = \{x\in C^m | Ax=0\}$$

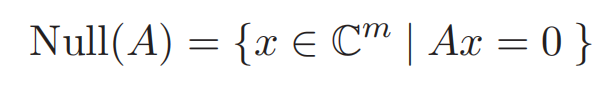
显然核是一种范围。

通俗来说：子空间的这个线性组合不仅取成矩阵A，而且经过A左乘之后得到零向量。

从直观上讲，A的零空间就是Ax=0的解空间。

此外，我们还有如下定理。

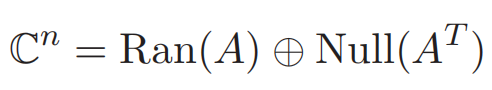
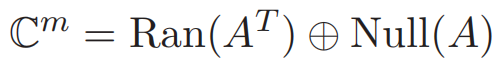
1.8 矩阵规范形式

什么是规约（reduction）：就是经过变换之后不改变特征值，但矩阵的形式更简单了（比如变成三角镇或者对角阵）。相似变换就是一种规约：

$$A = XBX^{-1}$$

则A和B是相似的。A与B的特征值相同。而且A与B的特征向量有关系：

$$u_A = X u_B$$

1.8.1 对角化

对角阵显然是最简单的。但是不是所有的矩阵都能三角化。有如下定理：

当且仅当矩阵有n个线性无关的特征向量时，才可以对角化。

还有个等价定理：

当且仅当矩阵有n个不等特征值的时候，可以对角化。

三角化不是唯一的。有约旦三角化和舒尔三角化。

1.9 正规和Hermitan矩阵

什么是正规（normal）：矩阵和它的共轭转置满足乘法交换律：

$$A^H A = A A^H$$

正规的性质：

任何正规阵都可以三角化。

不但如此，并且它的一组标准正交基就是Q的列向量。其中Q是舒尔规范形式中的Q。或者说是QR分解中的Q。

Hermitan矩阵是正规矩阵的一种特殊情况。具体来讲，

特征值为实数的正规矩阵就是Hermitan矩阵。

那么Hermitan矩阵有什么特殊的呢？

任何Hermitan矩阵都相似于一个实对角阵。

最后我们补充一下正定阵的定义：

假设一个实数矩阵满足：

$$(Au,u)>0, \forall u\in R^n, u \neq 0$$

那么A就是正定的。

也就是对任意非零向量u，Au和u的内积都大于0。

1.12 投影算子

投影算子就是一个等幂的线性变换（也就是自身不论乘多少遍自身都不变）。

$$P^2=P$$

显然（I-P)也是投影算子。因为I-P不论乘多少遍自身都不变。

而且一个巧妙的点是：任何向量都能拆成P和(I-P)的和

$$x=Px+(I-P)x$$

第二章 PDE离散

这章是走马观花地概述了PDE的离散化的三种方法：有限差分、优先体积、有限元。

并且还介绍了PDE椭圆方程（其实就是泊松方程）和对流扩散方程。

泊松方程算是最简单的一类PDE了。（如果右端等于0，还能简化为拉普拉斯方程）

二维椭圆方程（或泊松方程）就是：

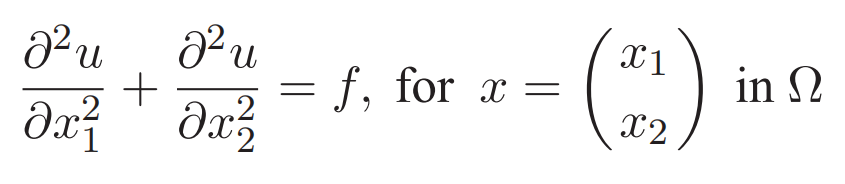
三类边界条件为：

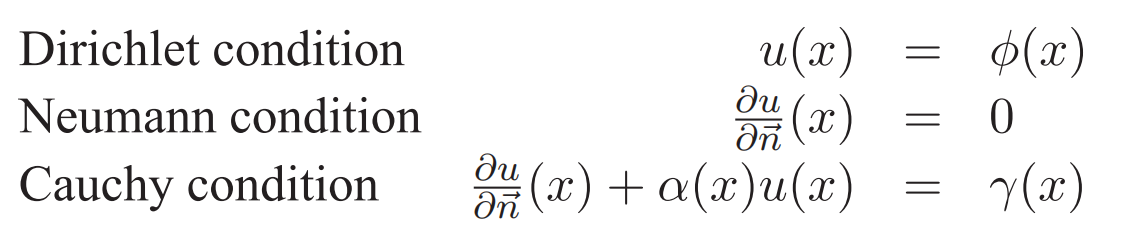
二维对流扩散方程就是

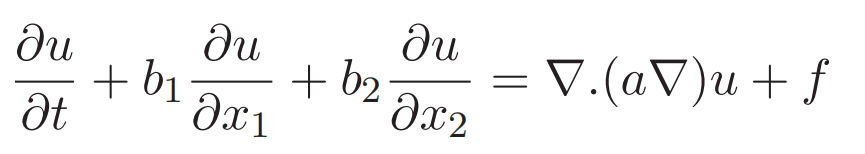
这个方程就差了一个压力项就是NS方程了。

求解的一个难点在于b可能是很大的，造成离散和求解的困难。

有限差分

前向后向和中心差分。拉普拉斯算子的离散。

迎风格式。

快速泊松求解器

有限元

散度定理

弱形式

伽辽金条件

有限体积

cell-centered cell-vertex

第三章 稀疏矩阵

按照课程表，我们只需要看3.1-3.5

3.1 引言

3.2 图表示

3.3 排列和重排序

3.4 存储方案

3.5 稀疏矩阵的基本操作

3.1 引言

稀疏矩阵是没有严谨定义的。只有个大致的说法：非零数很少的矩阵。正因如此，我们可以利用这个特点。首先是定义一种特殊的存储结构，从而节约内存。同时还可以利用该特性选择特定的数值方法，以达到最高效率。

与稀疏相对的当然就是稠密矩阵。稠密矩阵不太可能处理过大的矩阵，这也是为什么我们处理的叫做“大型稀疏线性系统”。

稀疏矩阵有两种：结构化的与非结构化的。顾名思义，结构化的就是其非零值位置是有规律的，比如在对角线附近。矩形网格上的有限差分法得到的矩阵是结构化的，而复杂几何的有限元或者有限体积法会得到非结构化网格。

结构化与非结构化对于直接解法来说没什么区别，但是对于迭代法来说，却非常重要。最简单的例子是矩阵向量乘法。对于结构化网格和非结构化网格的迭代法来说，效率差距很明显。

3.2 图表示

矩阵与图是可以相互表示的。这种矩阵也叫邻接矩阵。

当某个位置有非零值的时候，代表这里有一条边。

假如矩阵是对称的，意味着aij与aji是相等的。此时代表的就是无向图。

如图所示：上面的是非对称矩阵，对应有向图。下面是对称矩阵，对应无向图。

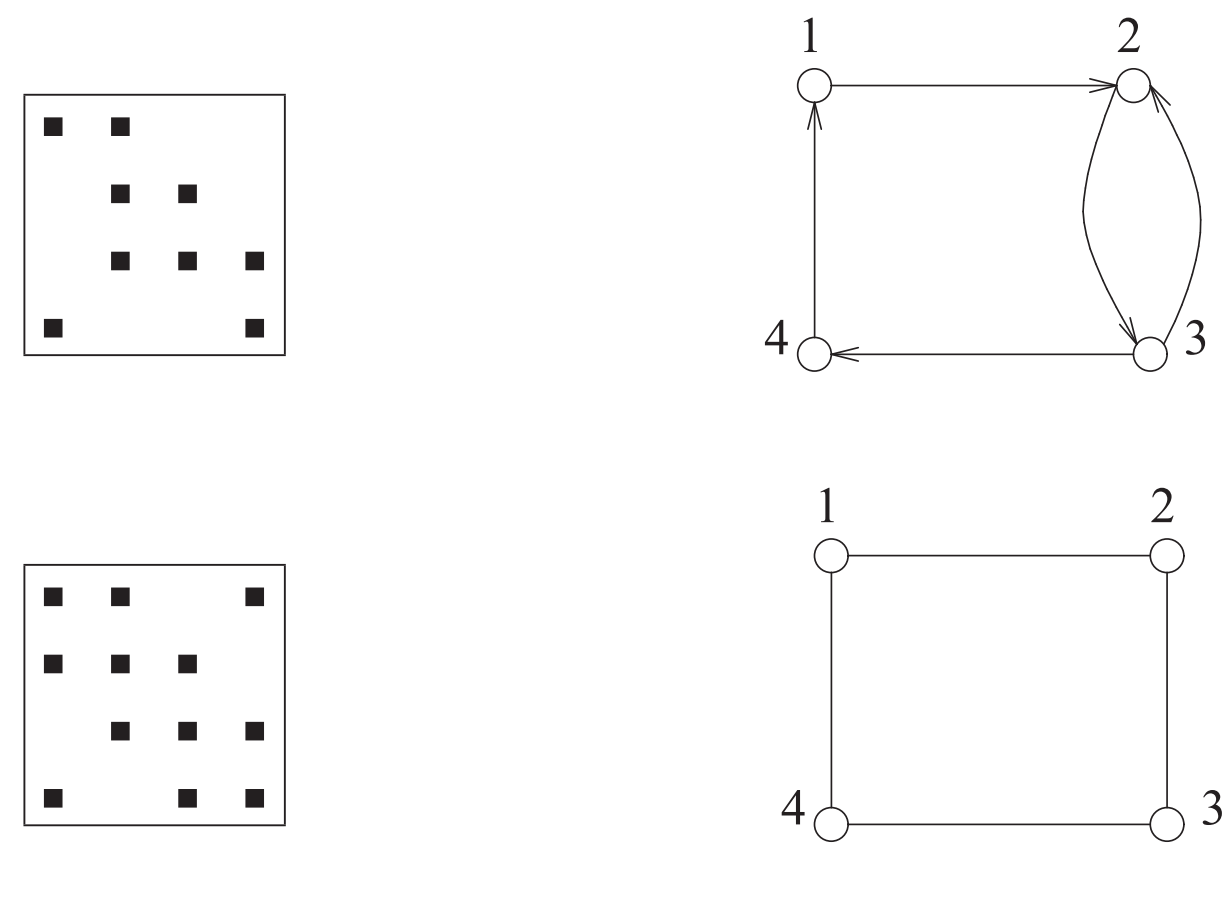
3.3 排列和重排序

这一节过长，我们放到后面再说

3.4 存储方案

坐标存储格式（Coordinate scheme）

一种比较简单存储稀疏矩阵的方案如下：

我们使用三个数组

1. 实数数组，存储非零值本身。（任意顺序）
2. 行下标数据
3. 列下标数据

一个例子：

这种方案的好处是非常简单直观，便于人类理解。因此软件包里通常会作为用户输入的"entry"。它也叫Coordinate scheme。

压缩系数行 Compressed Sparse Row

实际上，我们可以进一步节约内存。我们可以约定矩阵是按行存储的。也就是每一行从左到右存储（跳过零值）。存完一行再存一行。

由于每行存储的时候跳过0，我们需要知道每行有几个非零元素。或者，我们需要知道每行第一个元素的位置。这就用一个数组来存储。

同样由于跳过0，我们也需要知道每个非零元的列下标，这也用一个数组来存储。

于是上面的例子可以改写为

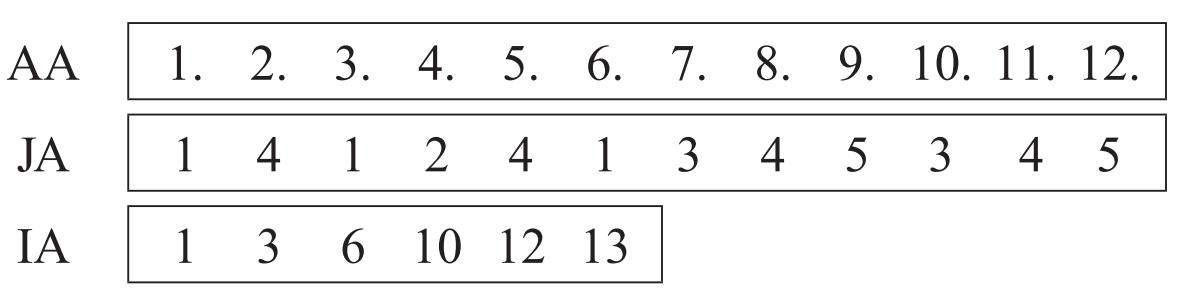
其中AA是非零元的数值本身（不要被例子的12345迷惑了，数值可以是任意的），它是第一个数组。是个实数数组。

JA是存储的列下标。它是第二个数组。它是整数数组。

IA存储的是每行开头的位置。比如3就代表第二行的第一个元素在AA中在第3个位置。6就代表第三行的第一个元素在AA中处于第6个位置。由于该例子数组AA中的数值恰好是从小到大排列的（再说一遍，不要被例子迷惑了，数值可以是任意的），因此看起来3恰好对应数值3.0，而6恰好对应数值6.0。

实际上，我们可以把IA的第一个元素位置换成是指针，道理也相同。这样就不需要开辟那么大的连续内存了。

这种存储方案是最流行的存储方案，它叫做压缩系数行格式（Compressed Sparse Row) CSR

改进的压缩系数行(Modified Compressed Sparse Row)

其实，CSR还能继续被优化。这种格式叫改进的压缩系数行（Modified Compressed Sparse Row） 格式。怎么改进呢？我们利用矩阵对角元通常不为0这个特性，可以把第三个数组合并到第二个数组里面。由于对角元的位置我们已经知道了。所以我们节约掉了IA，只需要两个数组即可。具体方法如下：

我们同时对照着下图的例子来看

先说AA：

1. AA先存对角元。存n个对角元到AA的前n个位置。注意：由于我们提前知道了他们一定是对角元，所以后面无需存储他们的位置。在例子里就是1，4，7，11，12。

2. 然后n+1的位置空出来。这个空通常留下来存一些有关矩阵的信息。例子里就是星号

3. 从AA的第n+2个位置开始按行存储非对角的非零元。一行存完再存一行。例子里就是2，3，5，6，7，9，10，12

然后说JA（JA无需存储对角元位置，只需要存储非对角非零元的位置）：

1. 前n行存储每行第一个非对角元在AA中所对应的位置。比如：首先是存第一行的第一个非对角元2的位置，它在AA中是第7个。然后是第二行的第一个非对角元3的位置，在AA中是第8个。然后是第三行的第一个非对角元6，它在AA的位置是10。以此类推。

2. n+1的位置重复第n个位置

3. 从第n+2的位置开始，存每个非对角元的列下标。比如：2对应列下标为4，3对应列下标为1，5对应列下标为4...

这个方案为什么能够节约掉IA呢？

因为其实它相当于节约掉了JA中前n个对角元的位置，然后把IA（也就是每行开头位置）挪到JA的前n个空里面。

对角方案

这个方案很简单，就是一条一条地存对角线（或对角线附近的次对角线）

例如：

DIAG数组有三列，每列对应一条对角线或次对角线。假如有空的位置就用星号代替。

IOFF存的是对角线的offset。也就是离主对角的距离。比如主对角下面的那个就是-1，主对角就是0，主对角上面的就是1

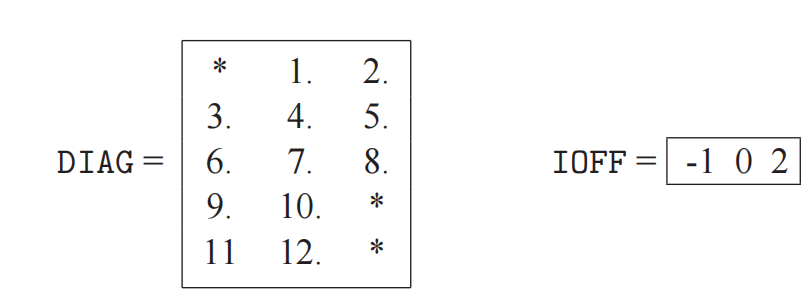
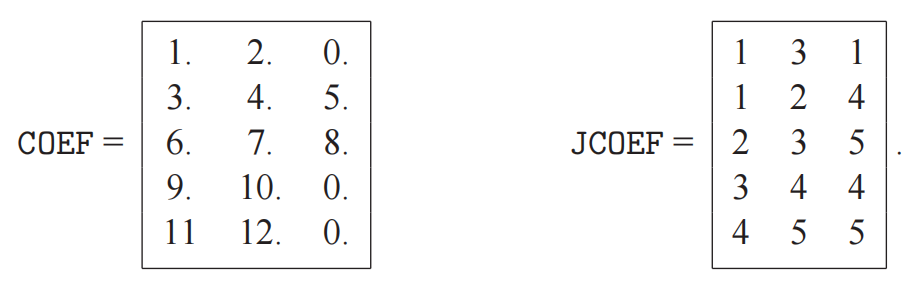
Ellpack-Itpack方案

这种方案在向量机中很流行。

COEF按行存元素。空的地方补0。

JCOEF存的是COEF中对应元素的列下标。

注意：COEF中相应的空的位置，被存成了行号，实际上这个位置是没用的，可以存任何数。但是书中说要是全存一样的数会对性能有影响。

3.5 系数矩阵的基本运算

基本就是向量、矩阵的乘法

第五章 投影方法

第六章 Krylov 子空间法I

由于这章太重要，所以大部分都要学。

重点有：

6.1-6.3

6.4，6.5.1，6.5.3-5， 6.7.1，6.11.3

第七章 Krylov 子空间法I

7.1-3，

7.4.1-2略读