最简单的FEM实现弹性

我们以最简短的方式总结下GAMES103里面linear FEM计算弹性的方法

slides:

https://games-cn.org/games103-slides/

太长不看版

$$\begin{bmatrix} \mathbf{f_1} & \mathbf{f_2} \end{bmatrix}= -A^{ref} \mathbf{F} \mathbf{S } \begin{bmatrix} \mathbf{X_{10}} & \mathbf{X_{20}} \end{bmatrix}^{-T}$$

2. $$F=\begin{bmatrix} x_{10} & x_{20} \end{bmatrix}\begin{bmatrix} X_{10} & X_{20} \end{bmatrix}^{-1}$$
3. $$S = 2 \mu G + \lambda trace(C) I$$

$$G = \frac{1}{2} (F^T F -I)$$

细节版本

以下均为二维情况（二维网格为三角形，三维是四面体）

我们从结果倒推

1. 我们要最终得到：施加到每个网格上的力 其中 Aref是reference state的三角形面积。F是deformation gradient, S是second piola-kirchoff stress。

$$\begin{bmatrix} \mathbf{f_1} & \mathbf{f_2} \end{bmatrix}= -A^{ref} \mathbf{F} \mathbf{S } \begin{bmatrix} \mathbf{X_{10}} & \mathbf{X_{20}} \end{bmatrix}^{-T}$$

2. F如何计算？

根据F的物理含义，它就是从reference state到current state的一个变换矩阵而已。因此我们可以先将点转化为距离（例如全部减去点0的坐标,其实就是rest length），然后根据下面的公式：current lenght 矩阵 乘以 rest len矩阵的逆 即可。

$$F=\begin{bmatrix} x_{10} & x_{20} \end{bmatrix}\begin{bmatrix} X_{10} & X_{20} \end{bmatrix}^{-1}$$

3. S如何计算？

使用StVK模型，得到应力与应变的关系。

注：我们的公式和物理量是拉格朗日视角下的，或者说叫以reference state作为参考坐标系的。

$$S = 2 \mu G + \lambda t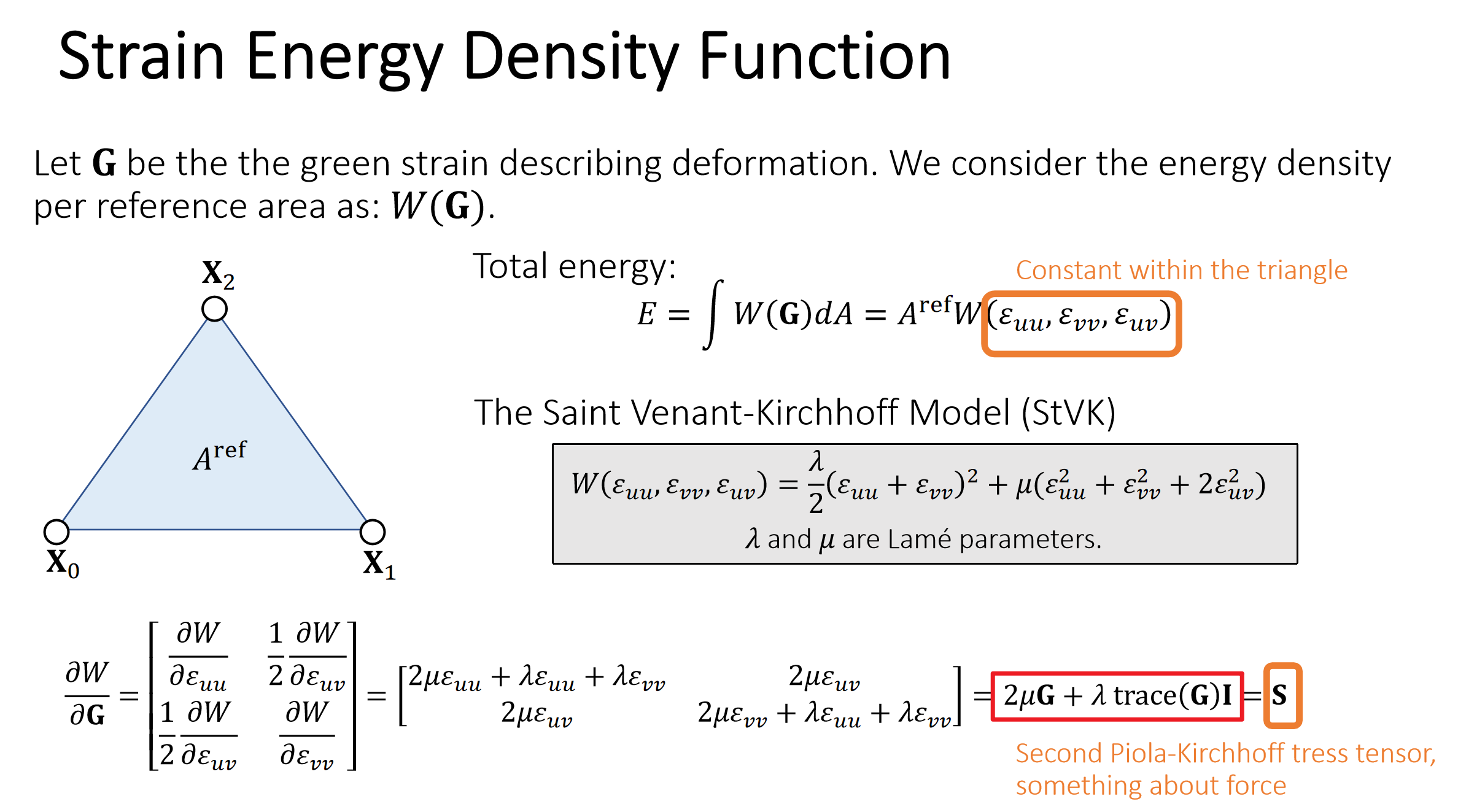race(C) I$$

其中G是格林应变

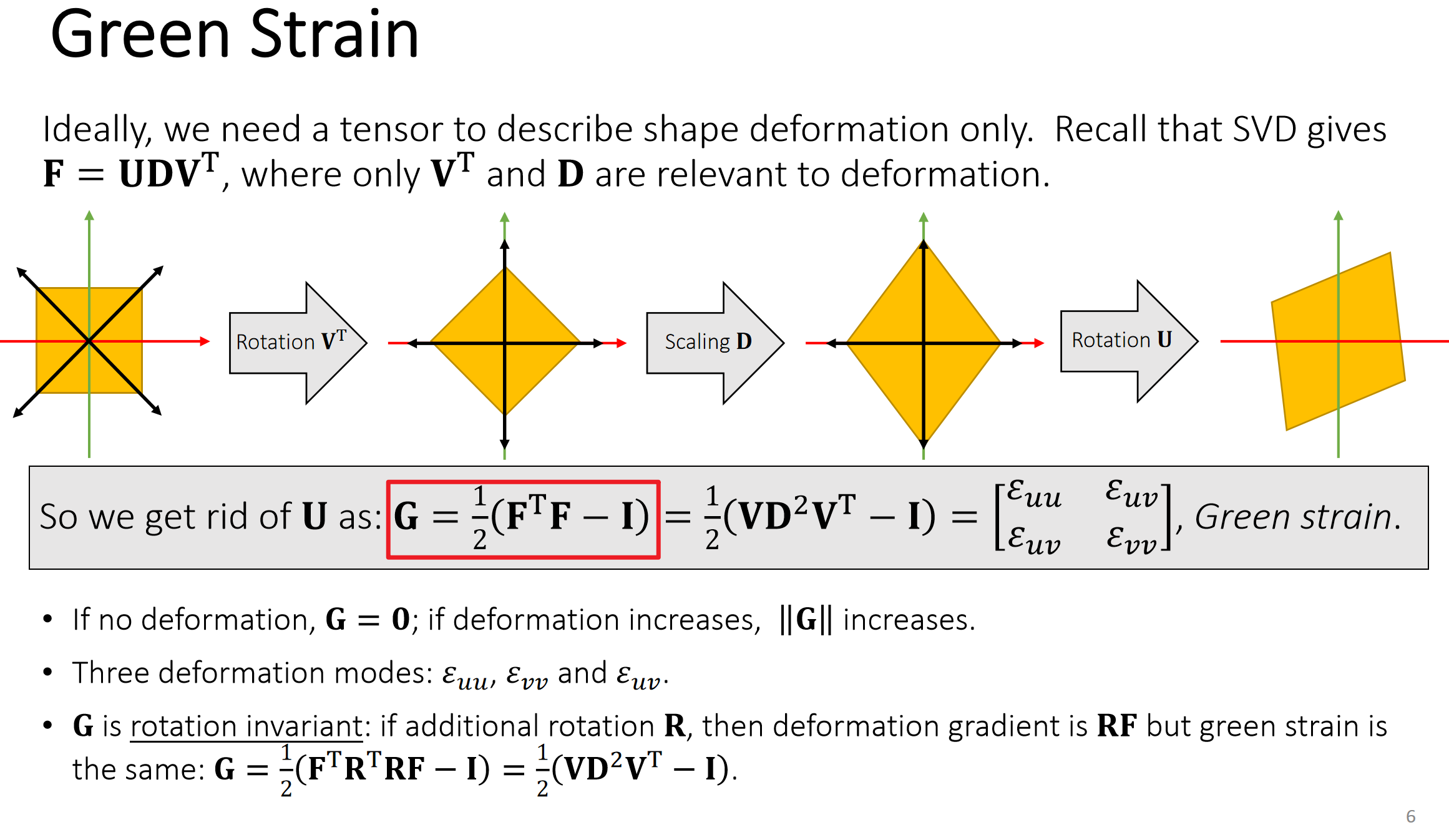
3. G如何计算？

$$G = \frac{1}{2} (F^T F -I)$$

（除了格林应变，我们还有柯西应变可以用。但柯西应变不满足旋转不变性，因此需要用SVD提取出来旋转）

格林应变的好处是其自动满足旋转不变性。