quternion

对应讲解视频

是什么：复数在三维的推广

四元数就是四个数。它是复数的推广。

复数为

a + bi

四元数则多了两个虚部

a + xi + y j + zk

其中i,j,k都是虚数。所以

i^2=j^2=k^2=ijk=-1

干什么的：三维点的旋转

复数表示二维旋转

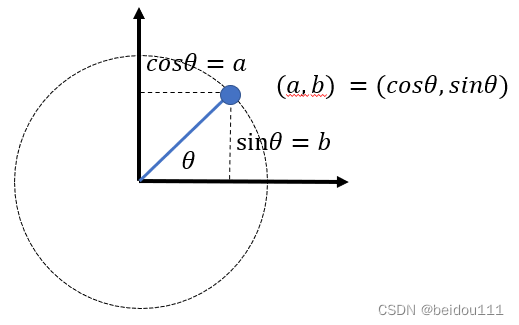
复数可以表示二维点的旋转。在这里插入图片描述

其中的圆是单位圆。

如图，就表示点或向量绕着原点旋转了 $\theta$ 角度。

我们可以把图中的二维坐标（a,b)写成一个复数

cos\theta + sin\theta \cdot i

四元数表示三维旋转

同理，四元数可以表示三维单位球面上的一个点（或者说是一个单位方向向量）的旋转

cos\theta/2 + sin\theta/2 \cdot (ai + bj+ ck)

这就表示绕着一个轴（a,b,c)（它是个单位向量）旋转 $\theta$ 角度。

为什么要用它：解决旋转矩阵的误差累积和欧拉角的万向节锁问题

在四元数之外，有另外两种表示三维旋转的方案：

欧拉角：简单易懂，但有万向节锁问题。
旋转矩阵：可以累乘，但有误差累计问题。

正是因为这两种表示方式的缺陷，才造成了四元数表示法的流行。

欧拉角的问题

欧拉角：即绕x轴，绕y轴，绕z轴旋转的角度。这三个角度叠加在一起，就能表示任意方向的旋转。

(\alpha, \beta, \gamma)

优点是简单直观，所以在三维软件的用户界面上通常都用欧拉角表示。但是软件内部的计算过程都用四元数。缺点是万向节锁问题。

万向节锁问题：就是两个转轴重合的时候，就会丧失其中一个旋转自由度。

旋转矩阵的问题

旋转矩阵用9个分量来表示旋转。当然它是对称的，因此实际上要存储6个分量。既然欧拉角只用了三个量，旋转矩阵的信息表示一定是冗余的。

冗余的信息干什么去了呢？冗余的信息用来表示剪切变形了。

也就是说，旋转矩阵并不只是用于刚体旋转的，剪切变形也掺混在旋转矩阵内部了。这就导致一个很严重的问题：当误差累积之后，旋转矩阵造成的误差效果不光是多转或少转了1、2度角度这么简单，而是造成了刚体的剪切变形！

剪切变形之后的刚体还是刚体吗？当然就不是了。这就是很严重的问题。

这也是为什么明明所有方法都会造成累积误差，但是我们特别在意旋转矩阵的累积误差的原因。因为它造成的后果很严重。

旋转矩阵要纯粹地表示刚体旋转，必须满足它是正交矩阵这个条件。如果不满足，那么它里面就掺杂了剪切变形！

因此我们每次旋转之后，需要将旋转矩阵正交化。其中一个正交化的方法，就是施密特正交化。你也许想象到了，施密特正交化是多么繁琐复杂的一个过程。

怎么做：用四元数旋转点

用旋转矩阵旋转点x，只要不断左乘矩阵就好了。

R_1R_2\mathbf{x}

而用四元数旋转点，则是要做个三明治：

q \mathbf{x}(q)^{-1}

这有点像矩阵相似，但是请注意相似矩阵的逆是写在左边的，而且，相似矩阵针对的是矩阵，这里的q是四元数。四元数的逆显然和矩阵的逆不是一个概念。四元数是复数的推广，不是矩阵！不能套用矩阵的运算法则。

幸好，四元数的逆非常简单，假设q为单位四元数（如果不是就先归一化）：

q^{-1} = w - ( ai+bj+ck)

这就是实部不变，虚部加个负号而已！而且你可以试验一下，它是否符合逆的概念，也就是 $qq^{-1}=1$

实际上，就是复数的共轭的推广。

PS: 如果q没有归一化，那么q的逆只需要再除以模的平方： $$ q^{-1} = \frac{w - ( ai+bj+ck)}{||q||^2} $$

旋转叠加

四元数也像旋转矩阵那样能够累乘！比如先旋转q1，再旋转q2

q_2(q_1 \mathbf{x}(q_1)^{-1})q_2^{-1} = (q_2q_1) \mathbf{x} (q_1^{-1}q_2^{-1})

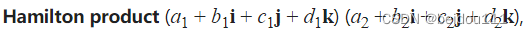
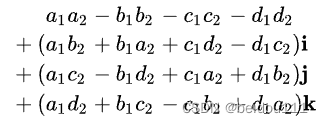
其中四元数的乘法非常简单，参考复数的计算方法就好了。在这里插入图片描述

在这里插入图片描述

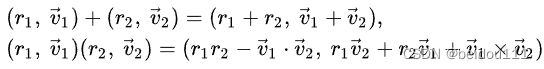
也可以参考下面的公式在这里插入图片描述

四元数转换为三维点

旋转之后，怎么得到三维的点坐标呢？

我们只需要把实部抛弃(或者写成0)，虚部的三个值恰好就是一个三维点的坐标。

也就是说

(0, xi+yj+zk)

恰好就是三维点

(x, y, z)

代码（C++ Eigen)

#include <Eigen/Dense>
#include <iostream>
#include <cmath>
using namespace Eigen;
using namespace std;
#define _MATH_DEFINES_DEFINED

//四元数相加
Quaternionf qadd(Quaternionf q1, Quaternionf q2)
{
    Quaternionf res;
    res.vec() = q1.vec() + q2.vec();
    res.w() = q1.w() + q2.w();
    return res;
}
//四元数数乘（即缩放）
Quaternionf qscale(Quaternionf q, float scale)
{
    Quaternionf res;
    res.vec() = scale * q.vec() ;
    res.w() = scale * q.w() ;
    return res;
}

//用向量公式的乘法 
Quaternionf qmul(Quaternionf q1, Quaternionf q2)
{
    Quaternionf res;
    res.vec() = q1.w() * q2.vec() + q2.w() * q1.vec() + q1.vec().cross(q2.vec());
    res.w() = q1.w() * q2.w() - q1.vec().dot(q2.vec());
    return res;
}

//用向量公式的乘法 （结果是一样的） 
Quaternionf qmul2(Quaternionf q1, Quaternionf q2) 
{
    Quaternionf res;
    res.w() = q1.w() * q2.w() - q1.x() * q2.x() - q1.y() * q2.y() - q1.z() * q2.z();
    res.x() = q1.w() * q2.x() + q1.x() * q2.w() + q1.y() * q2.z() - q1.z() * q2.y();
    res.y() = q1.w() * q2.y() - q1.x() * q2.z() + q1.y() * q2.w() + q1.z() * q2.x();
    res.z() = q1.w() * q2.z() + q1.x() * q2.y() - q1.y() * q2.x() + q1.z() * q2.w();
    return res;
}

//求逆
Quaternionf qinv(Quaternionf q) 
{
    Quaternionf res;
    res.vec() = - q.vec() ;
    res.w() = q.w();

    float n=q.norm();
    res.vec() /= n*n; 
    res.w() /= n*n; 
    return res;
}

int main()
{
    Quaternionf q1{1,2,3,4}, q2{5,6,7,8}, res;

    // cout<<q1 <<endl;
    // cout<<q2 <<endl;


    // res = qadd(q1, q2); //加法
    // cout<< res <<endl;


    // res =  qscale(q1, 5.0); //数乘
    // cout<< res <<endl;


    // cout<< q1*q2<<endl;  //Eigen自带乘法
    // res = qmul(q1,q2);   //乘法1
    // cout<< res <<endl;
    // res = qmul2(q1,q2);  //乘法2
    // cout<< res <<endl;


    // q1 = q1.normalized();
    // q2 = q2.normalized();


    // cout<< q1.inverse()<<endl;
    // res = qinv(q1);  //求逆
    // cout<< res <<endl;

    //用四元数旋转
    Vector3f point{1.0, 1.0, 0};
    point = point.normalized();
    Quaternionf p;
    p.vec() = point;
    p.w() = 0;

    float theta = 45.0 / 180 * 3.14159265358979323846;
    Vector3f axis{0,0,1};

    Quaternionf q{cos(theta/2), sin(theta/2) * axis[0], sin(theta/2) * axis[1], sin(theta/2) * axis[2]};
    cout<<q<<endl;

    Quaternionf p_new = q * p * q.inverse();
    cout<<p_new<<endl;

    Vector3f point_new=p_new.vec();
    cout<<point_new<<endl;
}

CMakeLists.txt

cmake_minimum_required(VERSION 3.10)
project(tryEigen)
find_package(Eigen3 REQUIRED)
add_executable(out tryEigen.cpp)

代码（numpy-quaternion)

有个python包（就叫numpy-quaternion）定义了常用的quaternion，代码库如下 https://github.com/moble/quaternion

文档如下 https://quaternion.readthedocs.io/en/latest/

安装

python -m pip install --upgrade --force-reinstall numpy-quaternion

导入

import numpy as np
import quaternion

定义四元数

q1 = np.quaternion(1,2,3,4) #定义一个四元数(w,x,y,z)
q2 = np.quaternion(5,6,7,8)
print(q1,q2.w, q2.x, q2.y, q2.z)
b = quaternion.as_float_array(q1) #转换为numpy数组
print(b)

输出

quaternion(1, 2, 3, 4) 5.0 6.0 7.0 8.0
array([1., 2., 3., 4.])

通过角度和转轴定义四元数

theta = np.deg2rad(90)  #转角：90度
axis = np.array([0,0,1])#转轴：z轴
q = np.quaternion(np.cos(theta/2), np.sin(theta/2) * axis[0], np.sin(theta/2) * axis[1], np.sin(theta/2) * axis[2]) #定义四元数：沿着转轴axis转theta角度
print(q)

theta1 = quaternion.as_euler_angles(q) #转换为欧拉角(常常不是预期结果, 慎用)
theta1 = np.rad2deg(theta1)
print(theta1)

输出

quaternion(0.707106781186548, 0, 0, 0.707106781186548)
[45.  0. 45.] #欧拉角的结果是不对的

转换为旋转矩阵后旋转一个点

point = np.array([1,0,0]) #定义一个点（1，0，0）
m  = quaternion.as_rotation_matrix(q) #四元数转换为旋转矩阵
## print(m)
v = m @ point #用旋转矩阵旋转一个点
print(v)

输出

[-2.22044605e-16  1.00000000e+00  0.00000000e+00]

直接用四元数旋转一个点

point = quaternion.from_vector_part(point) #将一个点转换为四元数，实部为0
print(point)
p_new = q * point * q.conjugate()   #旋转点，结果为四元数
print(p_new)
p_new = quaternion.as_vector_part(p_new) #结果四元数转换为点，直接去掉实部即可
print(p_new)

输出

quaternion(0, 1, 0, 0)
quaternion(0, 0, 1, 0)
[0. 1. 0.]

是什么：复数在三维的推广​

干什么的：三维点的旋转​

复数表示二维旋转​

四元数表示三维旋转​

为什么要用它：解决旋转矩阵的误差累积和欧拉角的万向节锁问题​

欧拉角的问题​

旋转矩阵的问题​

怎么做：用四元数旋转点​

旋转叠加​

四元数转换为三维点​

代码（C++ Eigen)​

代码（numpy-quaternion)​